堆 (Heap)

堆（Heap）是一种特殊的树形数据结构，通常实现为完全二叉树。在堆中，每个节点的值都大于或等于其子节点的值（最大堆），或者每个节点的值都小于或等于其子节点的值（最小堆）。这种特性使得堆在实现优先队列、排序算法等方面非常有用。

基本概念：

1. 最大堆 (Max Heap)：对于任何节点i，其父节点的值都大于或等于节点i的值。

2. 最小堆 (Min Heap)：对于任何节点i，其父节点的值都小于或等于节点i的值。

3. 完全二叉树：除了最底层，其他层次都是满的，最底层从左到右填充。

 

堆是一种满足以下条件的树：

堆中的每一个节点值都大于等于（或小于等于）子树中所有节点的值。或者说，任意一个节点的值都大于等于（或小于等于）所有子节点的值。

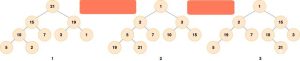
img

第 1 个和第 2 个是堆。第 1 个是最大堆，每个节点都比子树中所有节点大。第 2 个是最小堆，每个节点都比子树中所有节点小。

第 3 个不是，第三个中，根结点 1 比 2 和 15 小，而 15 却比 3 大，19 比 5 大，不满足堆的性质。

堆的分类

堆分为「最大堆」和「最小堆」。二者的区别在于节点的排序方式。

「最大堆」：堆中的每一个节点的值都大于等于子树中所有节点的值「最小堆」：堆中的每一个节点的值都小于等于子树中所有节点的值如下图所示，图 1 是最大堆，图 2 是最小堆

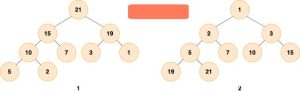
基本操作：

1. 插入：将新元素添加到堆的末尾，然后上移以维护堆的性质。

2. 删除：

   • 删除最大元素（对于最大堆）或最小元素（对于最小堆）。

   • 将最后一个元素移到根位置，然后下移以维护堆的性质。

3. 查找：

   • 查找最大元素或最小元素。

   • 查找特定元素或检查元素是否存在。

时间复杂度：

1. 插入和删除：O(log n)，其中n是堆中的元素数量。

2. 查找最大/最小元素：O(1)。

应用场景：

1. 优先队列：堆可以用于实现高效的优先队列，支持快速的插入、删除和查找操作。

2. 排序算法：如堆排序（Heap Sort）。

3. 调度和任务分配：在操作系统和计算机网络中优化资源分配。

优点：

1. 高效性能：堆支持快速的插入、删除和查找操作，具有对数时间复杂度。

2. 灵活性：堆可以动态增长和减少，适应不同大小和变化的数据集。

缺点：

1. 有限的查询操作：堆主要支持插入、删除和查找最大/最小元素，不适合频繁的随机访问操作。

2. 内存使用：堆可能需要额外的内存空间来存储指针或索引。

总结：

堆是一种强大而高效的数据结构，用于实现优先队列、排序算法等。通过保持其特定的性质，堆提供了快速、动态和灵活的数据管理和操作方法，使其成为解决各种计算问题和应用场景的理想选择。