图(Graph)
图(Graph)是一种非常重要的数据结构,用于表示对象之间的关系。图由节点(或顶点)和边组成,其中节点表示对象,边表示对象之间的关系。图在许多应用中都有广泛的用途,如网络设计、路由算法、社交网络分析、地图导航等。
图的基本概念:
-
节点 (Vertex 或 Node):图中的一个元素。节点可以表示任何类型的对象,如人、城市、交易等。
-
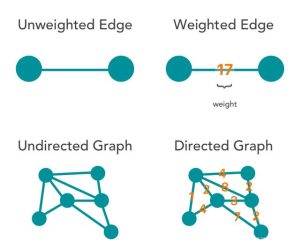
边 (Edge):连接两个节点的线段。边可以是有向的或无向的,有权的或无权的。
-
邻接:如果两个节点之间存在边,则它们被称为邻接节点。
图的分类:
-
无向图 (Undirected Graph):所有边都没有方向。
-
有向图 (Directed Graph 或 Digraph):边有方向,从一个节点指向另一个节点。
-
加权图 (Weighted Graph):边带有权重或成本。
-
稀疏图和稠密图:根据边的数量,图可以进一步分类为稀疏图(边的数量较少)和稠密图(边的数量较多)。
图的表示方法:
-
邻接矩阵 (Adjacency Matrix):使用二维数组表示节点之间的关系。对于无向图,矩阵是对称的;对于有向图,不一定对称。
-
邻接表 (Adjacency List):使用列表(如数组、链表)表示每个节点及其邻接节点。对于加权图,还可以存储边的权重。
基本操作:
-
添加节点和边:在图中添加新的节点和边。
-
删除节点和边:从图中删除特定的节点和边。
-
遍历图:访问图中的所有节点和边,常见的方法包括深度优先搜索 (DFS) 和广度优先搜索 (BFS)。
-
查找路径和最短路径:查找两个节点之间的路径,或者找到图中的最短路径。
应用场景:
-
网络设计和分析:如社交网络、Internet、通信网络等。
-
算法设计:如最短路径算法、图论算法、拓扑排序等。
-
数据结构和算法:图是许多高级数据结构和算法的基础,如树、堆、哈希表等。
总结:
图是一种较为复杂的非线性结构。
线性数据结构的元素满足唯一的线性关系,每个元素(除第一个和最后一个外)只有一个直接前趋和一个直接后继。树形数据结构的元素之间有着明显的层次关系。但是,树形结构的元素之间的关系是任意的。
「何为图呢?」「G(V,E)」,其中,G 表示一个图,V 表示顶点的集合,E 表示边的集合。
下图所展示的就是图这种数据结构,并且还是一张有向图。
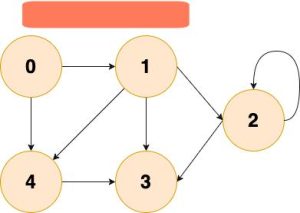
图
图在我们日常生活中的例子很多!比如我们在社交软件上好友关系就可以用图来表示。
图的基本概念
顶点
图中的数据元素,我们称之为顶点,图至少有一个顶点(非空有穷集合)
对应到好友关系图,每一个用户就代表一个顶点。
边
顶点之间的关系用边表示。
对应到好友关系图,两个用户是好友的话,那两者之间就存在一条边。
度
度表示一个顶点包含多少条边,在有向图中,还分为出度和入度,出度表示从该顶点出去的边的条数,入度表示进入该顶点的边的条数。
对应到好友关系图,度就代表了某个人的好友数量。
无向和有向
边表示的是顶点之间的关系,有的关系是双向的,比如同学关系,A 是 B 的同学,那么 B 也肯定是 A 的同学,那么在表示 A 和 B 的关系时,就不用关注方向,用不带箭头的边表示,这样的图就是无向图。
有的关系是有方向的,比如父子关系,师生关系,微博的关注关系,A 是 B 的爸爸,但 B 肯定不是 A 的爸爸,A 关注 B,B 不一定关注 A。在这种情况下,我们就用带箭头的边表示二者的关系,这样的图就是有向图。
无权和带权
对于一个关系,如果我们只关心关系的有无,而不关心关系有多强,那么就可以用无权图表示二者的关系。
对于一个关系,如果我们既关心关系的有无,也关心关系的强度,比如描述地图上两个城市的关系,需要用到距离,那么就用带权图来表示,带权图中的每一条边一个数值表示权值,代表关系的强度。